すみさんのゲームを真面目に考えてみる

2018年3月2日

すみさんはこのようなミニゲームを考えました。

【ミニゲーム】6面ダイスを好きな個数だけ同時に振って良い。
出た目の合計が得点となる。ただし1個でも1の目が出ていたら得点は入らない。
これを繰り返して得点の合計が180点に達したら勝ち。

このルールの時にサイコロを最初にいくつ振るのが正解でしょうか。
(期待値が一番高くなるサイコロの個数はいくつか。)

答え

サイコロの個数をｎとする。

n=1の時、
1/6*0+1/6*2+1/6*3+1/6*4+1/6*5+1/6*6=20/6=10/3≒3.33

分子の20は２から６までの和ということに注目する。

n=2の時、

	１	２	３	４	５	６
１	✕	✕	✕	✕	✕	✕
２	✕	４	５	６	７	８
３	✕	５	６	７	８	９
４	✕	６	７	８	９	10
５	✕	７	８	９	10	11
６	✕	８	９	10	11	12

これらの数値の総和は200のため、
200/36=50/9≒5.56

これを２から６が10回ずつ足されていることに注目する。
つまり20*10=200が分子となる。

n=3の時、

２が３個重複するのは１通り(全て２の場合)
２が２個重複するのは４*３通り(2-2-X,2-X-2,X-2-2)
２が１個重複するのは16*３通り(2-X-X,X-X-2,X-2-X)

つまり、

4^(n-k)* nCk *k …① の kを１からｎまで動かした時の総和となる(∑)

∴75となり75*20/216=125/18≒6.94 となる。

だんだん大きくなってきた。

n=4の時、

式①の総和は500となる。

どうやらn*5^(n-1)と等しいようである。

つまり、一般式としてｎ個の時の期待値は
(1/6)^n * 20 * n * 5^(n-1)となる。

簡単にすると (5/6)^n * 4n となる。

グラフにプロットすると次のようになる。

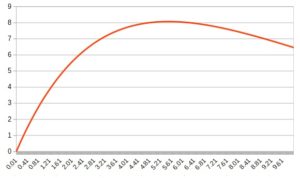
個数は自然数なので蛇足だがn=5.48の時最大値8.071となるようである。
(微分は難しいため、妥協した。)

n=5の時、8.037551
n=6の時、8.037551 というのが最大となる。

よって答えは５または６(個)

(の時に大体８くらいでるんじゃない？)

ただし、５個の場合で60％、６個の場合で67％近く１が１つは出るので注意。
運が悪ければ０から全く増えなさそう。